The Combo Pricing Trap: A Regression Story – Simply Explained

🍟 Scene: College Canteen – Evening Chai Time

Varun and Rohit walk up to the counter, fries sizzling and chai boiling in the back.

Varun: I’m grabbing chai for both of us. Want anything else?

Rohit: I’m starving, bro. I’ll treat myself to the burger combo.

Varun: Haha, no worries — it’s on me. I still owe you from the last bet.
(to the vendor) Two combos, bhaiyya!

Menu says – Fries + Burger + Large Soft Drink – ₹120

Rohit: Thanks, man. My treat next time! 🤗 Honestly, combos just hit different. They feel more worth it.

Varun (grinning): Ever wonder why that is? This meal just walked us into a regression concept.

Rohit: Seriously? Not even here? 😄 Okay, what now?

Varun: Think about the ₹120. Why not ₹150 or ₹100? There’s data behind that number.

Rohit: Alright, hit me.

Varun: It’s all about customer preferences. Let me ask — what happens to burger sales when fry sales go up?

Rohit: Both go up, I guess?

Varun: Exactly. That’s positive correlation. When sales of one rise, so do the other.

Rohit: Bro, I’m just getting into this, and you’re already dropping “positive” correlation 😵‍💫

Varun: My bad 😄. So — correlation just tells us how strongly two things move together.
If both increase or decrease together — that’s positive correlation.
If one goes up while the other goes down — that’s negative correlation.

Rohit: Got it… but sounds like there’s math behind it?

Varun: There is, but let’s skip the formulas for now. Just know correlation values go from -1 to 1.
+1 means perfect positive, -1 is perfect negative — but those extremes rarely happen in real life.

Rohit: Cool. Your graphs help more than the math — here, take this paper napkin.

Varun: Haha, deal.

📈 Varun sketches a quick scatter plot on the napkin

Each dot = a day of sales. Burger sales on one axis, fries on the other.

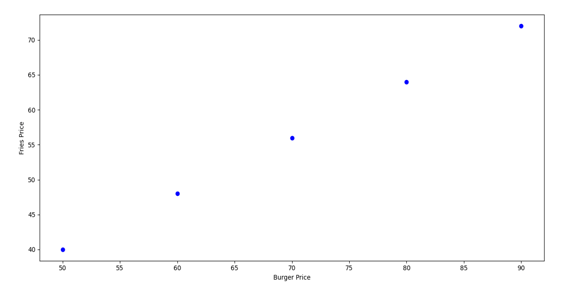
Varun: See how the dots rise diagonally? That’s positive correlation — more burgers sold means more fries too.

Rohit: Oh! So that makes pricing easier, right?

💡 Enter the pricing puzzle

Varun: Not really. Here’s the catch — when two items are positively correlated, their prices also rise together.

Rohit: So if people like both, shouldn't setting a price be easy?

Varun: You’d think so. But let’s look at this:

🧮 Positively Correlated Preferences

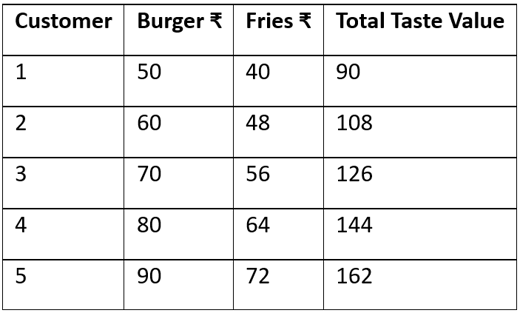
Varun: Their tastes move together. But now, you need to fix a combo price that works for everyone.
What if someone loves burgers but is just “meh” on fries — or vice versa?

Rohit: You’re stuck. One price won’t please everyone, so you’ll lose a few customers.

Varun: Exactly. When tastes rise together, they also spread out.
Picking a single combo price becomes risky — too high for some, too low for others.

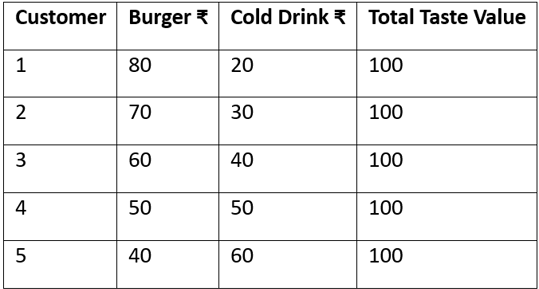
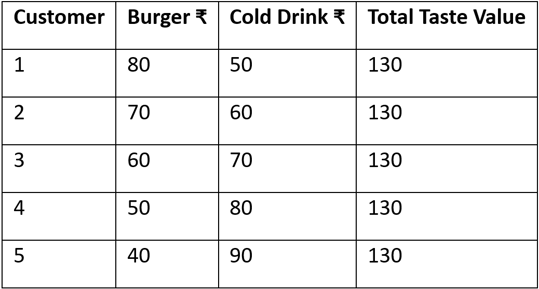
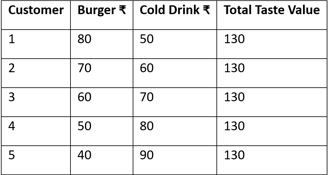
✅ Negatively Correlated Preferences

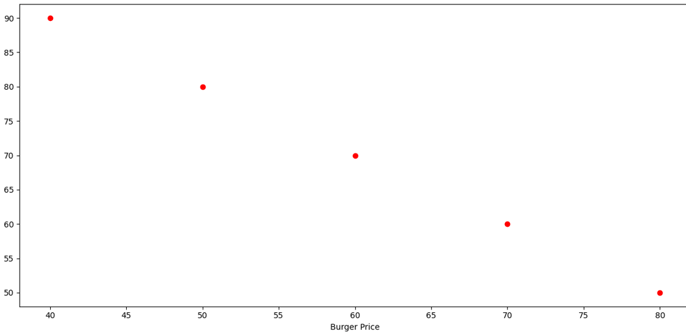
Varun: Now flip it — imagine people who love burgers don’t care for cold drinks, and vice versa.

Varun: Here, as one value goes up, the other drops — negative correlation.
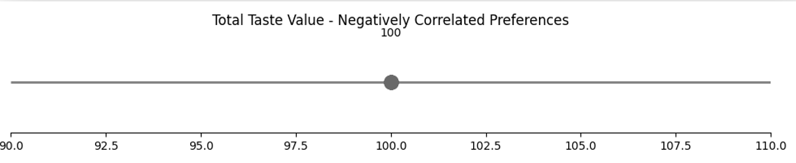
But notice — the total stays fixed at ₹100.

Varun: Here, as one value goes up, the other drops — negative correlation.
But notice — the total stays fixed at ₹100.

Rohit: So now, it’s easier to set a combo price?

Varun: Bang on. Just price it around ₹100, and everyone’s covered.
Way less guessing, way more satisfaction.

✅ Bundling & Perceived Surplus

Varun (still sketching): Now check this out — people value the two items differently, but always total ₹130.

Varun: Say cold drinks cost ₹90 alone. But you, a burger fan who values it at ₹80, get both in a combo for ₹120.
How does that feel?

Rohit: Like I’m getting the drink for just ₹40! Even though it’s priced at ₹90. That’s a deal.

Varun: Exactly. That’s perceived surplus.
And guess what — the cold drink lover feels the same, just the other way around.

Rohit: So everyone feels like they’re winning?

Varun: Yep. That’s the magic of bundling when products are negatively correlated.
You don’t need perfect individual prices — just one smart combo price.

🥡 Wrapping it Up

Rohit: So bundling works best when the items are negatively correlated?

Varun: Not always, but it’s way easier to price smartly when tastes balance each other out.
Regression helps companies see those patterns — even in something as simple as a combo meal.

Rohit: I swear, I can never eat in peace with you 😄

Varun: You mean learn in bites.

📘 Why This Blog Matters

This is Part 4 of the Simply Explained Regression Series.
In earlier parts, Rohit explored regression, scatter plots, line fitting, and overfitting.
Here, we take that understanding further by showing how correlation impacts combo pricing.

Key Takeaways:

• Positive correlation increases spread — hard to price combos fairly.

• Negative correlation stabilizes totals — easier, smarter pricing.

• Bundling + perceived surplus = value felt by all.

👉 Coming up next: How do you know if your regression model is “good”?

We’ll dive into model quality, residuals, and real-world decision-making.